Lab 11

The purpose of the lab was to get the Bayes filter working on the real-robot. For this task, we were given an optimized Bayes filter that would run faster. We were then supposed to use that optimized Bayes filter in order to do the localization using distance measurements from the robot.

Optimized Bayes Filter

We were given an extra localization_extra.py file that contained optimized versions of the Bayes filter functions that we were required to write within Lab 10. I looked at these and it appears that the functions are optimized in order to run faster. I tested out the optimized Bayes filter in the simulator first just to see how well it worked.

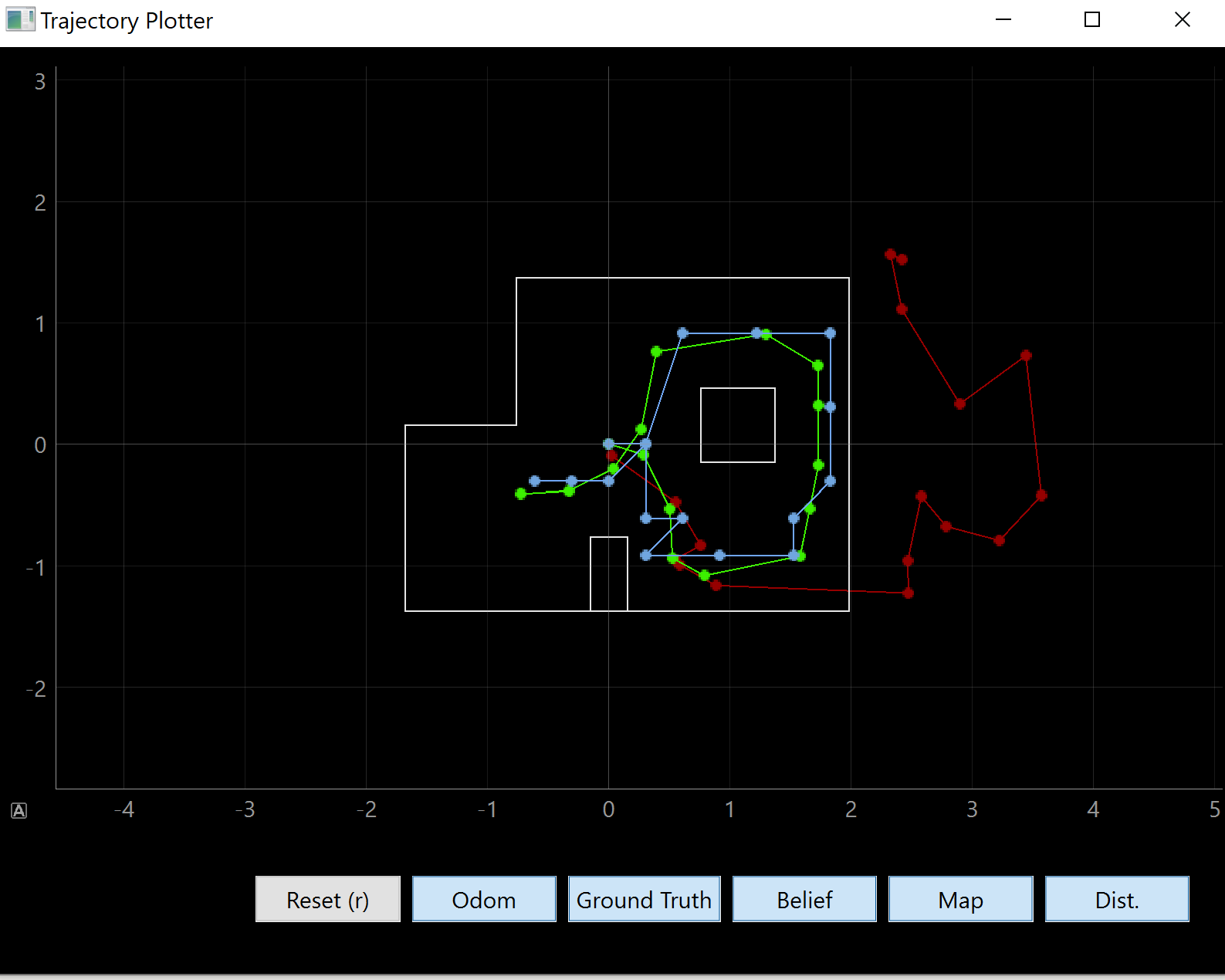
As we can see, it is pretty accurate and tends to be within the same grid cell or at least 1 grid cell away.

Observation Loop

The given task is similar to Lab 9, the mapping lab. However, I took measurements in 15 degree increments while in this lab, we were supposed to take measurements in 20 degree increments. It was a simple task of changing the for() loop to stop at 20 degree increments instead of 15. Other than that, I changed it so that my robot would not send the data asynchronously, but it would send it over immediately after finishing collecting the measurements. This made the coding easier on the Python side, as I could simply check the length of the Python array that I stored my distance measurements in (using the notification handler) and have the Python program sleep while it was empty. The last change I made was with the notification handler. Because the perform_observation_loop() function is part of the RealRobot() class, I had my distance and yaw arrays become attributes of the RealRobot class and had the notification handler update my RealRobot()’s distance and yaw arrays.

Below is the Python code for perform_observation_loop()

async def perform_observation_loop(self, rot_vel=120):
        """Perform the observation loop behavior on the real robot, where the robot does  
        a 360 degree turn in place while collecting equidistant (in the angular space) sensor
        readings, with the first sensor reading taken at the robot's current heading. 
        The number of sensor readings depends on "observations_count"(=18) defined in world.yaml.
        
        Keyword arguments:
            rot_vel -- (Optional) Angular Velocity for loop (degrees/second)
                        Do not remove this parameter from the function definition, even if you don't use it.
        Returns:
            sensor_ranges   -- A column numpy array of the range values (meters)
            sensor_bearings -- A column numpy array of the bearings at which the sensor readings were taken (degrees)
                               The bearing values are not used in the Localization module, so you may return a empty numpy array
        """
        self.distances = [];
        self.yaw = []
        
        #The first two values are Kp,Ki,Kd, then setpoint, then base speed"
        ble.send_command(CMD.SET_VEL,"1.5|0.1|65|0|0")
        
        await sleep_for_1_secs()
        await sleep_for_1_secs()
        await sleep_for_1_secs()
        
        ble.send_command(CMD.PID,"1")
        
        while(len(self.distances) < 20):
            await sleep_for_1_secs()
        robot.distances = [x/1000 for x in robot.distances]
        mod_x = np.zeros(18)
        mod_x[0] = robot.distances[17]
        mod_x[1:18] = robot.distances[0:17]
        x = np.array([mod_x]).T
        y = np.array([robot.yaw[0:18]]).T
        return x, y
        raise NotImplementedError("perform_observation_loop is not implemented")

Note that I had to rearrange my yaw array because my measured distance values were offset from the measured yaw values by 1 position in each array, which is that weird chunk of code in the middle. I also had to convert millimeters to meters (which was the source of much of my troubles) and also had to make sure it was stored within a column array (which was the source of the rest of my troubles)

Performing the observation loop

Here is a video of the robot performing one of the observation loops.

Note that I wasn’t really able to get the robot to turn on-axis. I believe this is because of the very large difference between my motor drivers, where it turns out that the offset factor between my two wheels actually depends on the PWM value I put in. Essentially, it’s not a linear offset and so depending on the speed, the wheels won’t drive at the same power. In a previous lab, I figured out that when it drives slow, the offset factor is about 0.57. However, this is also affected by battery power. When I incorporate this difference into the code, the only way for the robot to turn on-axis is to have it drive a little bit faster, but that results in the robot overshooting the angle by a little bit. This adds up, and the robot will take measurements at the incorrect angle. I believe that it is more important for the robot to not turn on-axis and have the measuresments at the correct angle than to turn on-axis and have the incorrect depth measurements. However, this will most likely lead to some error as we can see in the following graphs.

We were told to localize at 4 different points (in feet):

• (-3, -2)

• (0,3)

• (5,-3)

• (-5, -3)

Here are photos of the plots from the simulator plotter:

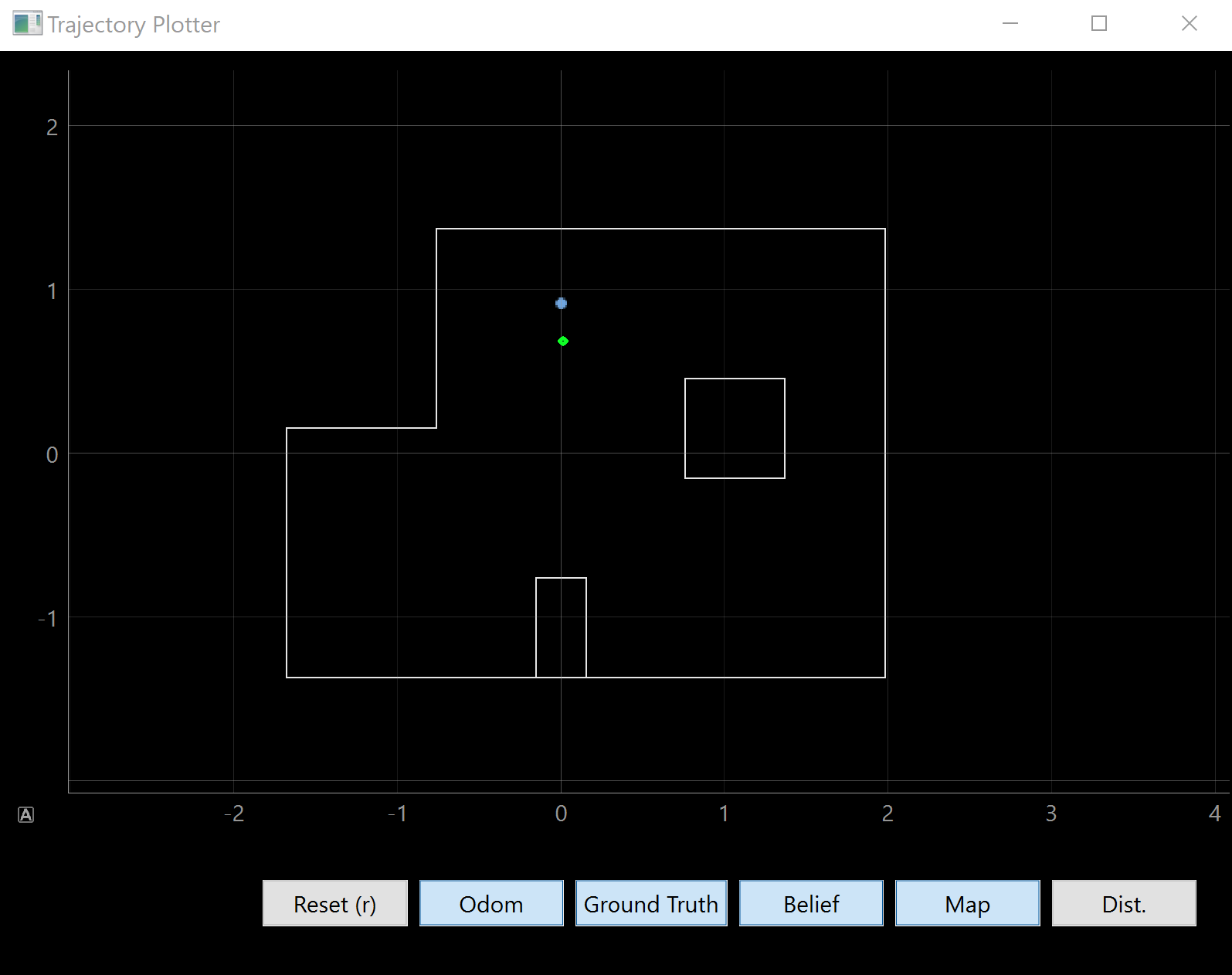
(0,3)

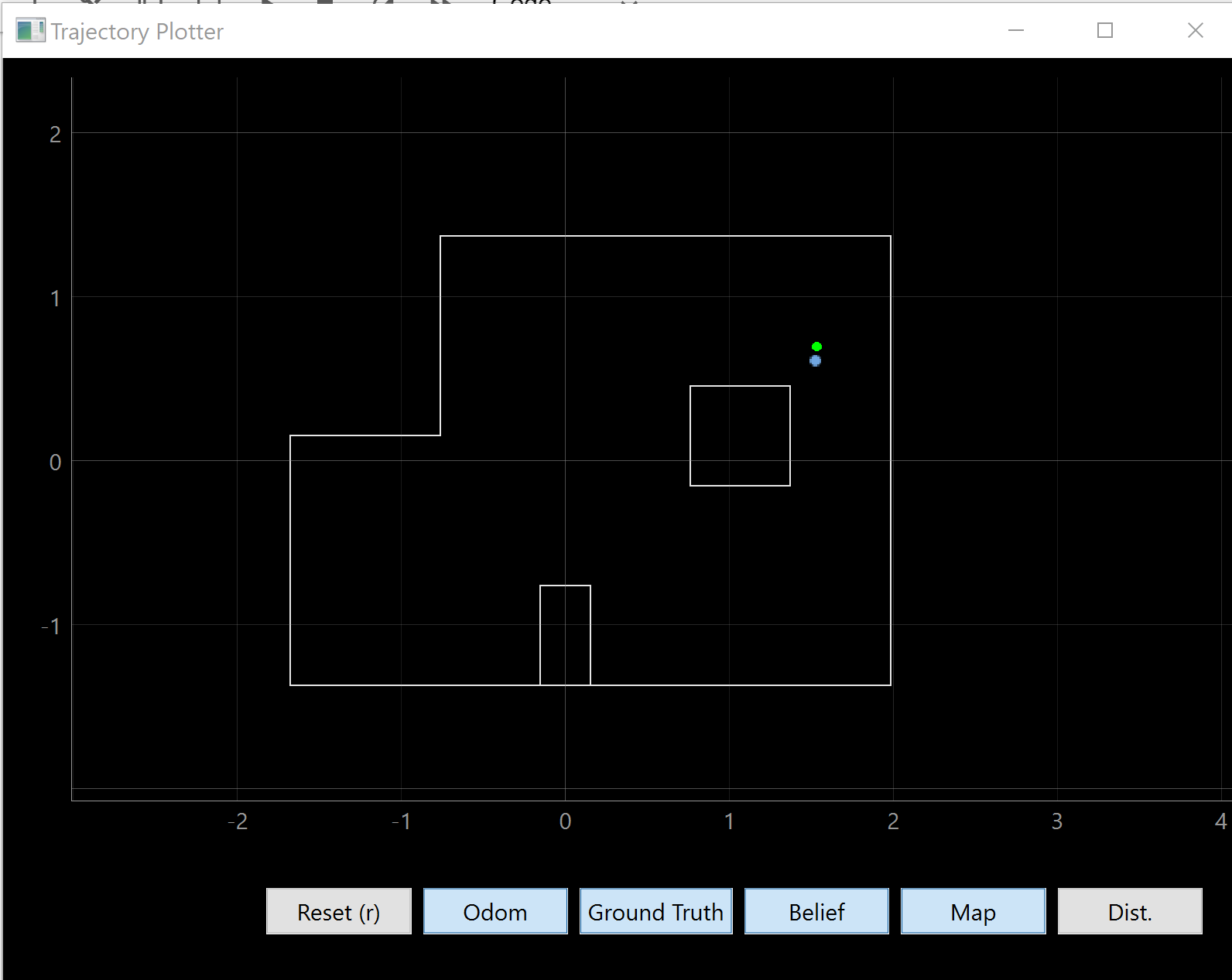
(5,3)

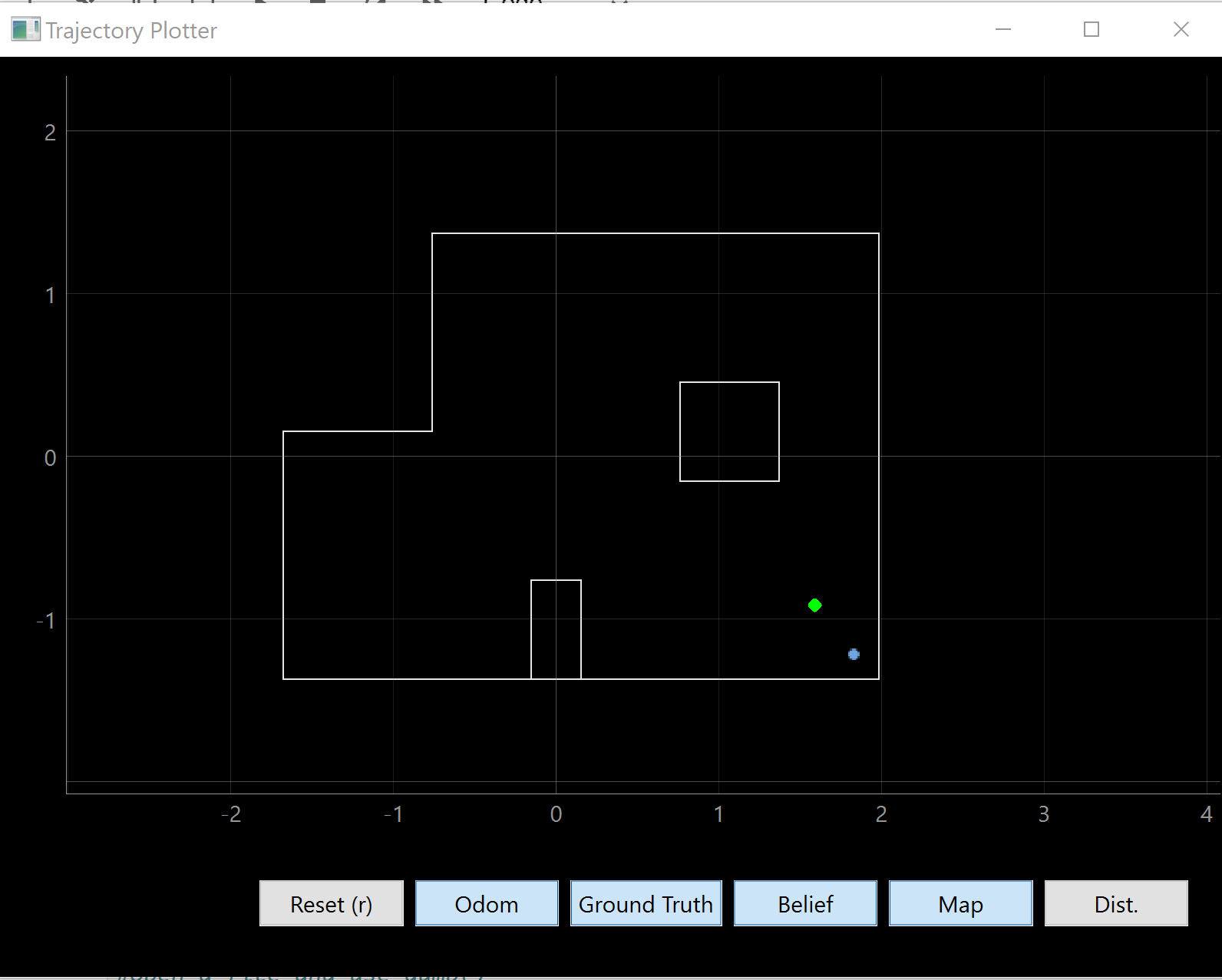
(5,-3)

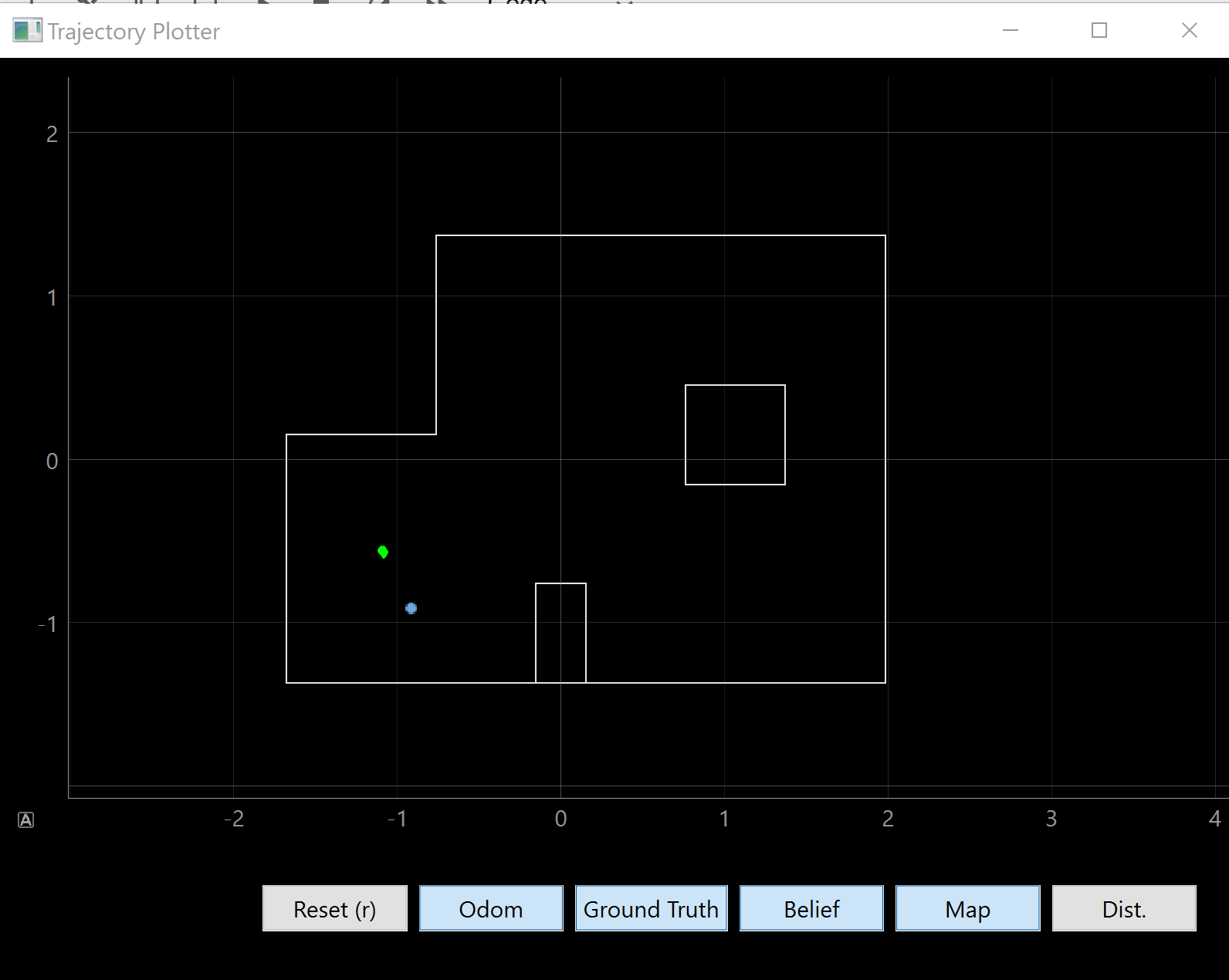
(-3,-2)

As we can see, most of them are pretty close to the correct one. There are a few reasons why the localization may not be perfect. I believe the main reason is that my robot did not turn on axis, meaning that the distance measurements are not all from the same spot as my distance sensor will move around. Thus, if my robot turns and it starts taking measurements from another grid cell, then the Bayes filter will also place some belief in those grid cells as well. We can see the effects of this from the localization at (5,-3), which is where the video was taken as well. As the robot turns counter-clockwise, it takes a lot of measurements which are closer to the wall and because these measurements are less noisy, they are more accurate. This means they have a greater effect on the belief (since we have a larger P(z

x)) would cause the robot to localize closer to the walls.

Another reason is the symmetry of certain positions. While most of these spots are pretty unique, a few of them are more similar than others. For example, (5,-3) and (0,3), both have two walls and a few boxes behind them. However, because the ToF sensors are not as accurate at long ranges, the two walls that are closer will have a greater effect on the Bayes filter.