Lab 12

In this lab, we were given the task of visiting a list of waypoints within the space. We were allowed to do the task in any method we wanted. Because I was fortunate enough to have already had built a PID controller for orientation and distance from the wall, I decided to use this approach in order to completely this task.

Waypoints

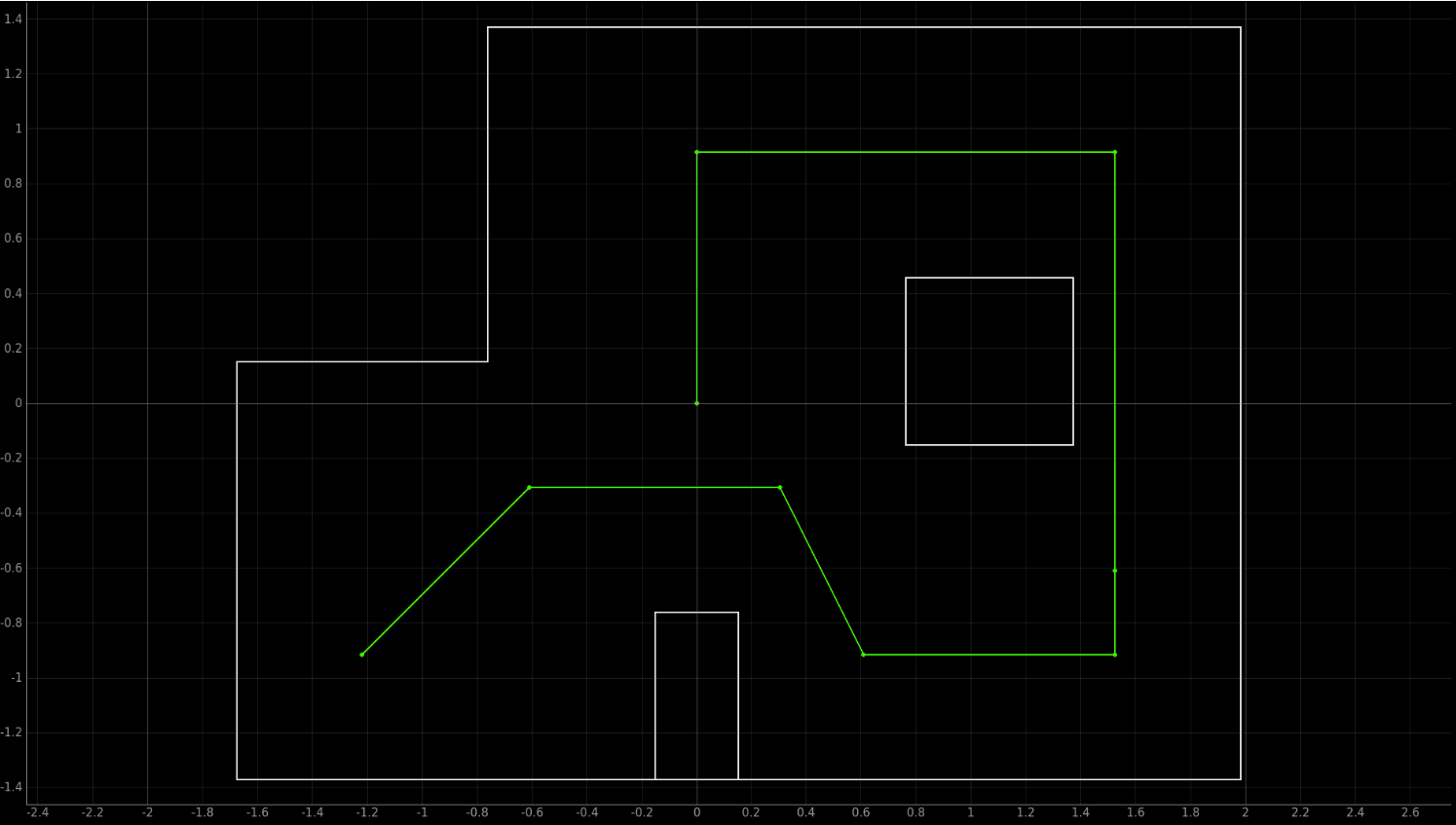
The list of given waypoints (in feet) were:

(-4, -3)
(-2, -1)
(1, -1)
(2, -3)
(5, -3)
(5, -2)
(5, 3)
(0, 3)
(0, 0)

I have attached the given plot that shows the placement of these waypoints within the map below:

sdf

Actuating my robot

My strategy was pretty straight-forward. In terms of controlling the robot, I would use PID control to control the angle my robot turns and would use a P controller to control the distance from the wall in front of it. That way, I could the P controller to control how far my robot moved in a pretty accurate manner. Thus, in theory, my robot should be able to turn to any angle and drive forward any distance in a pretty accurate manner.

Orientation PID controller

I had already built a pretty robust orientation PID controller for both Lab 8 and Lab 9. I simply had to tune my orientation PID controller values a little bit to have the turns be a little bit smoother (though this was mostly for personal preference and the values I used for Lab 8 worked perfectly fine). In the end, my Kp = 3, Ki = 2, and Kd = 1. The basis of my orientation PID controller is pretty simple: drive the robot forward at some base speed by turning left/right wheels separately. Then, subtract some offset from the speed at which I drive my right/left wheels that will redirect the robot towards the setpoint. If we use a base speed of 0, the robot will (theoretically, as we found out in Lab 11), turn on-axis by driving right and left wheels at opposite PWM values. However, if our base speed is some value, like x for example, the robot will drive forward in a straight line when yaw is close enough to the setpoint, but will turn towards the setpoint when the robot yaw goes too far away. Thus, I was able to make my robot drive straight at any speed I wanted without having to worry about the difference between the motor drivers for right/left wheels. The final code I used for PID orientation control is below:

void PID_orientation(float dt, float speed){
  //Comment out the updating time thing for the stunt
  // current_time = millis();
  // float dt = (current_time - prev_time)/1000;
  // prev_time = current_time;

  if(myICM.dataReady()){
    myICM.getAGMT();
  }
  yaw = yaw + myICM.gyrZ() * dt;

  error_ = (yaw) - set_point;

  d_error = (error_ - prev_error)/dt;
  prev_error = error_;
  if((a_error<360 || a_error>-360)){
    a_error = a_error + error_ * dt;
  }
  

  control = abs(kp * error_  + ki * a_error + kd * d_error);
  
  if(control < min_speed){
    control = min_speed;
  }
  if(control > 255){
    control = 255;
  }

  if(abs(error_) < 3){
    control = 0;
    a_error = 0;
  }
  if(yaw < set_point){
    right_speed = speed + control; 
    left_speed = speed - control;
    if(right_speed > 255){
      right_speed = 255;
    }
    if(left_speed > 255){
      left_speed = 255;
    }
    if(right_speed < -255){
      right_speed = -255;
    }
    if(left_speed < -255){
      left_speed = -255;
    }

    right_wheels(right_speed);
    left_wheels(left_speed);
  }
  else{
    left_speed = speed + control;
    right_speed = speed - control;
    if(right_speed > 255){
      right_speed = 255;
    }
    if(left_speed > 255){
      left_speed = 255;
    }
    if(right_speed < -255){
      right_speed = -255;
    }
    if(left_speed < -255){  
      left_speed = -255;
    }
    right_wheels(right_speed);
    left_wheels(left_speed);
  }
}

void right_wheels(int speed){
  if(speed > 0){
    analogWrite(13,abs(speed));
    analogWrite(11,0);
  }  
  else if(speed < 0){
    analogWrite(11,abs(speed));
    analogWrite(13,0);
  }
  else{
    analogWrite(13,0);
    analogWrite(11,0);
  }
}

void left_wheels(int speed){
  if(speed > 0){
    analogWrite(6, abs(speed));
    analogWrite(7,0);
  }  
  else if(speed < 0){
    analogWrite(7, abs(speed));
    analogWrite(6,0);
  }
  else{
    analogWrite(6,0);
    analogWrite(7,0);
  }
}

Distance P controller and moving forward a set distance

I also used a P controller to control my distance from the wall directly in front of my robot. This would allow my robot to travel forward at any distance I wanted by setting the setpoint to be current_distance - distance_to_travel. This, fortunately, worked with negative distances as well, allowing my robot to back up whenever I wanted it to as well.

I only used a P controller because I felt it was more important to be accurate than fast for travelling straight distances for my robot. Thus, I made the speed at which the robot moved 55 at all times in terms of PWM values so it wouldn’t overshoot the setpoint too much, but also wouldn’t hit deadband. I suppose this means that technically, it is not even a P controller, but it worked for my purposes. This meant that an integrator/derivative term was unnecessary as my robot was not moving forward at a speed which would cause it to overshoot and there wouldn’t be any deadband for the integrator term to fight. I also used the PID orientation control in order to ensure my robot moved forward in a straight line. My Kp value was 0.3.

Below is the integrated code which allows the robot to move a set distance.

if(dance_val){
              current_time = millis();
              dt = (current_time - prev_time)/1000;
              prev_time = current_time;

              if(distanceSensor1.checkForDataReady()){
                distance = distanceSensor1.getDistance();
                if(distance == 0){
                  distance = distance + velocity * dt;
                }
                float dt_velocity = (current_time - previous_time_dist)/1000;
                velocity = (distance - previous_dist) / dt_velocity;
                previous_time_dist = millis();
                previous_dist = distance;
                distanceSensor1.clearInterrupt();
                distanceSensor1.stopRanging();
                distanceSensor1.startRanging();                                
              }
              else{
                distance = distance + velocity * dt;
              }
              float d_error = distance - stop_distance;
              speed = (int)(kp_d * d_error);
              Serial.println(speed);
              Serial.println(d_error);  
              if(speed > 55){
                speed = 55;
              }
              if(speed < -55){
                speed = -55;
              } 
              if(speed > 0 && speed < 55){
                speed = 55;
              }
              else if(speed < 0 && speed > -55){
                speed = -55;
              }

              PID_orientation(dt,speed);

              if(abs(d_error) < 13 && !stop_move){
                stop_time = millis() + 2000;
                stop_move = true;
              }
              if(millis() > stop_time){
                dance_val = false;
                distanceSensor1.stopRanging();
                stop_robot();
              }
            }

Original Strategy

For actually traversing, my original strategy was going to be:

Localize where the robot is and update pose (unless we are at the start. Then, we know where our robot starts)
Compute distance to travel and angle to turn to move to the goal waypoint based on robot pose.
Turn angle, then move distance.
Relocalize. and update pose If we are at the next waypoint, update the goal waypoint to be the next waypoint in the list. Else, do not do that and continue to try to move to the current goal waypoint.
If we have finished with list of waypoints, stop robot.

However, a few issues popped up that made me scrap localization early on. First, my robot still had issues turning on-axis consistently. This, coupled with the fact that my front Time-of-Flight (ToF) sensor was not the greatest sensor and gave pretty noisy measurements, meant that my robot was only able to localize correctly about 50% of the time (and about 20% of the time in certain spots of the map). We can see this with Lab 11. If I wanted my robot to succeed, it would need to localize correctly a lot more times than that, probably at least 90%. If my robot localized incorrectly, then my robot would receive incorrect movement commands and that could lead into my robot crashing into obstacles, which would almost lead to certain failure. I did not want my runs to be dependent on my robot localizing correctly a majority of the time when my robot would consistently localize incorrectly half the time.

Another issue I had was with actually actuating my robot. In theory, if my robot could see the wall directly in front of it (so at \(\theta\) = 0 in robot reference frame), then it could move any distance it wanted in that direction. However, in the map, there were occasionally spots where my robot could not see the wall in front of it because it was too far away. I have no idea why, considering I kept my ToF sensor in long mode at all times. It still was consistently an issue, messing up many times and many runs, including a near perfect run as we’ll see later. Thus, I found the best course of action in these cases was to actually turn and face the opposite way (so 180 - \((\theta)_t\)) and move the negative distance based of the wall behind the robot, which was usually a lot closer. However, based off of robot pose alone, there is no way to actually know when I should drive backwards and when I should drive forwards without some complicated function. I thought of using a function that can compute the distance from a point to the wall that was in front of/behind of it, but that would have been a lot of extra math. Thus, if I did not localize and simply used my PID/P controllers, which I tuned to be very accurate, I could simply hard-code whether to drive backwards or forwards. However, this means that in localization, where I don’t necessarily know where my robot is before executing the control loop, it is not possible to know whether I should drive my robot forwards/backwards.

This was also an issue with the very first point I had to visit after the starting waypoint. For this one, instead of moving backwards, I hard-coded it to use Manhattan distance. This was mostly to demonstrate two forms of moving from point to point, but it also made moving to the first point much more consistent. Computing controls for this was pretty simple, since the angles to turn were now 90 degrees and the distances to move were \(\Delta x\) and \(\Delta y\).

## Updated Strategy (I don’t why this heading won’t compile as a heading)

After deciding not to use localization, I decided to make it so that my robot would use one set of control actions (angle to turn and distance to travel) to move from one point to the next, minus the first point since I used Manhattan distances for that one. The strategy is as follows

If just starting off, use Manhattan distances to travel from the starting location to the first point
After reaching first point, update pose to be first point.
Start looping through waypoints here:
Based on pose, compute control (angle to turn and distance to travel).
Execute control (either while moving forwards or backwards, which was hard-coded)
Update pose to be the next waypoint for x and y, and update theta based on control actions taken.
If no more points, we are done!

This strategy is not exactly open-ended (i.e, it cannot take any list of waypoints), as I needed to hard-code certain movements to be forwards or backwards based on qualitative observations of if my robot could see the wall in front of it, and I added Manhattan distance. However, if my robot had a better ToF sensor on the front that could see the walls in front of it, then it could easily be an open-ended solution, and the issues that make it not open-ended are not the algorithm itself, but issues with my hardware.

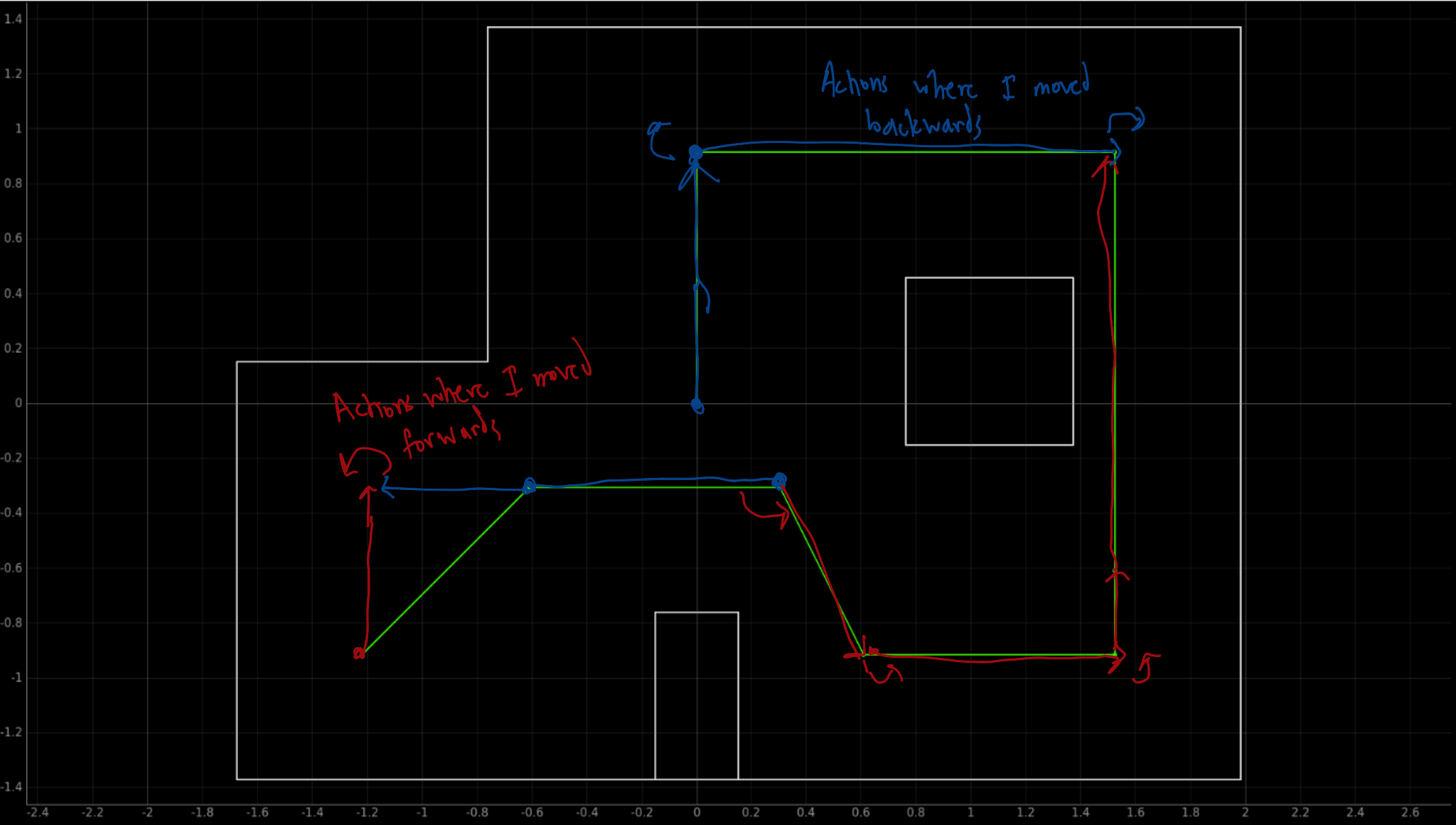
Diagram: sdfdsdfsd

Below is the Python cell that did this:

waypoints = np.array([[-1.2192,-0.9144, 0], [-0.6096,-0.3048, 0], [0.3048,-0.3048, 0], [0.6096,-0.9144, 0],[1.524,-0.9144, 0], [1.524,-0.6096, 0], [1.524, 0.9144, 0], [0, 0.9144, 0], [0,0,0]])
# Note that my waypoints have been converted to meters for ease of use.
dimensions = np.shape(waypoints)
offset = 0.9
await asyncio.sleep(3)
for i in range(dimensions[0] - 1):
    if(i ==0):
        # Hard coded first point
        pose = waypoints[i][:].copy()
        next_waypoint = waypoints[i+1][:].copy()
        #Should be facing x-axis
        ble.send_command(CMD.TURN,"90")
        await asyncio.sleep(3)
        
        #Now facing y-axis
        dist_to_travel = round((next_waypoint[1] - pose[1]) * (1000 ))
        cmd_string = "1|" + str(dist_to_travel)
        print(cmd_string)
        ble.send_command(CMD.DANCE,cmd_string)
        await asyncio.sleep(5)
        
        ble.send_command(CMD.TURN,"90")
        await asyncio.sleep(3)
        
        # Now facing x-axis again
        dist_to_travel = -1 * round((next_waypoint[0] - pose[0]) * (1000))
        cmd_string = "1|" + str(dist_to_travel)
        print(cmd_string)
        ble.send_command(CMD.DANCE,cmd_string)
        await asyncio.sleep(5)
        
        # ble.send_command(CMD.TURN,"-180")
        # await asyncio.sleep(3)
        pose = next_waypoint.copy()
        pose[2] = 180;
    else:
        # Move to the rest of the points
        next_waypoint = waypoints[i+1][:].copy()
        print("Current Waypoint: ", pose)
        print("Next Waypoint: ", next_waypoint)
        [turn_angle, travel_dist, sdf] = loc.compute_control(next_waypoint, pose)
        turn_angle = round(turn_angle) + 11
        
        travel_dist = round((travel_dist) * (1000 * offset))
        if(i == 1):
            turn_angle = 0
            travel_dist = -1 * travel_dist
        if(i == 3):
            turn_angle = turn_angle + 5
        if(i == 6 or i == 7):
            turn_angle = 180 - turn_angle
            travel_dist = -1 * travel_dist
        if turn_angle != 0:
            ble.send_command(CMD.TURN, str(turn_angle))
            await asyncio.sleep(3)

        cmd_string = "1|" + str(travel_dist);
        print(cmd_string)
        ble.send_command(CMD.DANCE,cmd_string)
        await asyncio.sleep(5)
        
        print("Turn Angle: ", turn_angle)
        print("Travel Dist: ", travel_dist)
        pose[0:2] = next_waypoint[0:2].copy()
        pose[2] = pose[2] + turn_angle

An almost successful run (and how I generally debugged)

Below is an almost successful run, where I miss the very final waypoint (this is after many, many attempts).

As we can see, my turn and move scheme works really well. My PID controller is able to turn the angles pretty accurately and my P controller can move distances pretty accurately. I found that adding some offsets to the control actions helped. This was most likely due to how I determined when I was close enough to the setpoint for my PID controllers. However, I included this video to show the issue with my robot not being able to see the wall in front of it to determine its initial distance.

A successful run!

Here is a successful run, where I was able to hit every waypoint. Unfortunately, I accidentlly missed the very first action. However, as we can see from my almost successful run, it was able to do it. I stop at most of them on the dot, which is really nice. My failed attempt actually was better for most of the initial waypoints but failed the last waypoint so oh well :(.

Overall, I really enjoyed my solution. Because my robot was able to have really accurate control actions, I was able to traverse the map without localizing. Thus, my robot was able to believe it was at the next waypoint after every control sequence. Thus, the plot for my robot’s belief would be: sdfsd

If I had more time, I would implement localization so that my robot can correct itself if it goes off course.

My entire Arduino file:

My entire Python notebook: